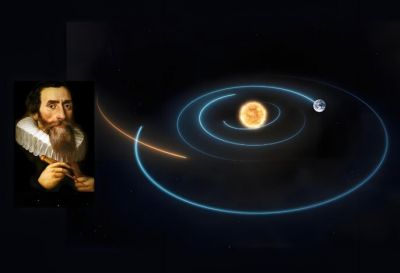
開普勒定律，又稱開普勒三定律或行星運動定律，是描述行星繞太陽公轉運動規律的三大定律。這三條定律由德國天文學家約翰內斯·開普勒基于丹麥天文學家第谷·布拉赫的觀測數據，通過長期的分析和研究，于1609年至1619年間提出。開普勒定律不僅徹底推翻了托勒密的地心說，還完善并簡化了哥白尼的日心說，對天文學的發展產生了深遠影響。

第谷·布拉赫被譽為“星子之王”，他在天體觀測領域取得了卓越成就，留下了長達20多年的觀測資料和一份精密星表。開普勒作為第谷的助手，繼承并利用了這些寶貴的觀測數據，致力于編制新星表。然而，在編制火星運行表時，開普勒發現按照正圓軌道計算始終無法與觀測數據吻合。經過無數次的分析和計算，他大膽提出火星軌道為橢圓的假設，并最終證實了這一觀點，從而發現了行星運動的第一定律。

開普勒第一定律（橢圓定律）

每個行星都沿各自的橢圓軌道環繞太陽運行，而太陽則位于橢圓的一個焦點上。這一發現打破了長期以來天體運動必須為正圓的觀念，為天文學的發展開辟了新的道路。

開普勒第二定律（面積定律）

在相等的時間內，太陽與行星的連線所掃過的面積相等。這一定律揭示了行星公轉過程中的角動量守恒原理，表明行星在靠近太陽時速度加快，遠離太陽時速度減慢。

開普勒第三定律（調和定律）

行星公轉周期的平方與其橢圓軌道半長軸的立方成正比。這一發現為后來牛頓提出萬有引力定律奠定了基礎，使得人們能夠從物理學的角度解釋行星的運動規律。

開普勒定律的數學證明涉及復雜的微分方程和幾何語言。以開普勒第一定律為例，通過設定太陽與行星的質量、位置矢量等參數，利用牛頓第二定律和角動量守恒原理，可以推導出行星在同一平面內沿橢圓軌道運動的結論。而開普勒第二定律和第三定律的證明則進一步揭示了行星公轉過程中的速度和周期與軌道參數之間的定量關系。

牛頓在其著作《自然哲學的數學原理》中，應用第二定律和萬有引力定律，在數學上嚴格證明了開普勒定律，并賦予了其深刻的物理意義。他指出，行星之所以沿橢圓軌道運動，是因為受到了來自太陽的引力作用。這一發現不僅解釋了行星的運動規律，還為后來的天文學和宇宙學研究提供了重要的理論基礎。

開普勒在發現行星運動定律的過程中遇到了諸多挑戰。他不僅要面對傳統觀念的束縛，還要克服計算上的困難。然而，他憑借堅定的信念和不懈的努力，最終成功打破了勻速圓周運動的偏見，提出了橢圓軌道和等面積定律等創新觀點。這些觀點的提出不僅徹底摧毀了托勒密的本輪系，還為哥白尼的日心說帶來了充分的完整性和嚴謹性。

開普勒定律

開普勒定律在天文學和物理學領域具有深遠的科學意義。首先，它表現出了無比勇敢的創造精神，否定了長期以來天體運動必須為正圓的觀念，為天文學的發展開辟了新的道路。其次，它徹底摧毀了托勒密的本輪系，解放了哥白尼體系，使其更加完整和嚴謹。最后，它使人們對行星運動的認識得到了明晰的概念，證明了行星世界是一個勻稱的系統，受來自太陽的某種統一力量所支配。

此外，開普勒定律還為后來的天文學和宇宙學研究提供了重要的理論基礎。它啟發了牛頓等科學家尋找太陽系結構的奧秘，為經典力學的建立和萬有引力定律的發現作出了重要提示。可以說，開普勒定律是天文學發展史上的一個重要里程碑。

開普勒定律適用于宇宙中一切繞中心天體運動的天體，包括行星、衛星等。在宏觀低速天體運動領域，開普勒定律具有普遍意義。然而，對于高速的天體運動或涉及多個中心天體的復雜系統，開普勒定律可能需要進一步的修正和擴展。盡管如此，開普勒定律仍然是我們理解天體運動規律的重要工具之一。

開普勒定律的發現是天文學發展史上的一個重要里程碑。它不僅徹底改變了人們對行星運動的認識，還為后來的天文學和宇宙學研究提供了重要的理論基礎。隨著科學技術的不斷進步和觀測手段的不斷完善，我們有理由相信，在未來的天文學研究中，開普勒定律將繼續發揮重要作用，并為我們揭示更多宇宙的奧秘。