胡克定律是力學中的一項基本定律，描述了彈性體在受力作用下的變形規律。它由英國科學家羅伯特·胡克在17世紀末提出，并且至今仍然被廣泛應用于力學領域。表示為：應力后固體材料中的應力和應變（單位變形量）之間成線性關系。1]滿足虎克 的定律被稱為線彈性或胡克式（英文胡克）材料。

胡克定律

從物理學的角度來看，虎克 定律源于大多數固體（或孤立分子）里面的原子在沒有外載的情況下處于穩定平衡的狀態。許多實用的材料，如長度為l、胡克 s定律可以用來模擬截面積為3354的棱柱桿的單位伸長率（或縮減）量（應變）在常系數E（稱為彈性模量）下，與拉（或壓）應力σ成正比，即：F=-k·x或△F=-k·Δx。其中為總伸長（或縮減）量。

胡克 羅伯特，一位17世紀的英國物理學家，使用了萬有引力定律·胡克的名字命名。胡克提出這個定律的過程相當有趣1676年，他發表了一個拉丁縱橫字謎，謎語是：ceiiinosssttuv。兩年后，他宣布答案是：ut tensio sic vis，意思是“力如伸長（那樣變化）這是虎克的中心內容的法律。

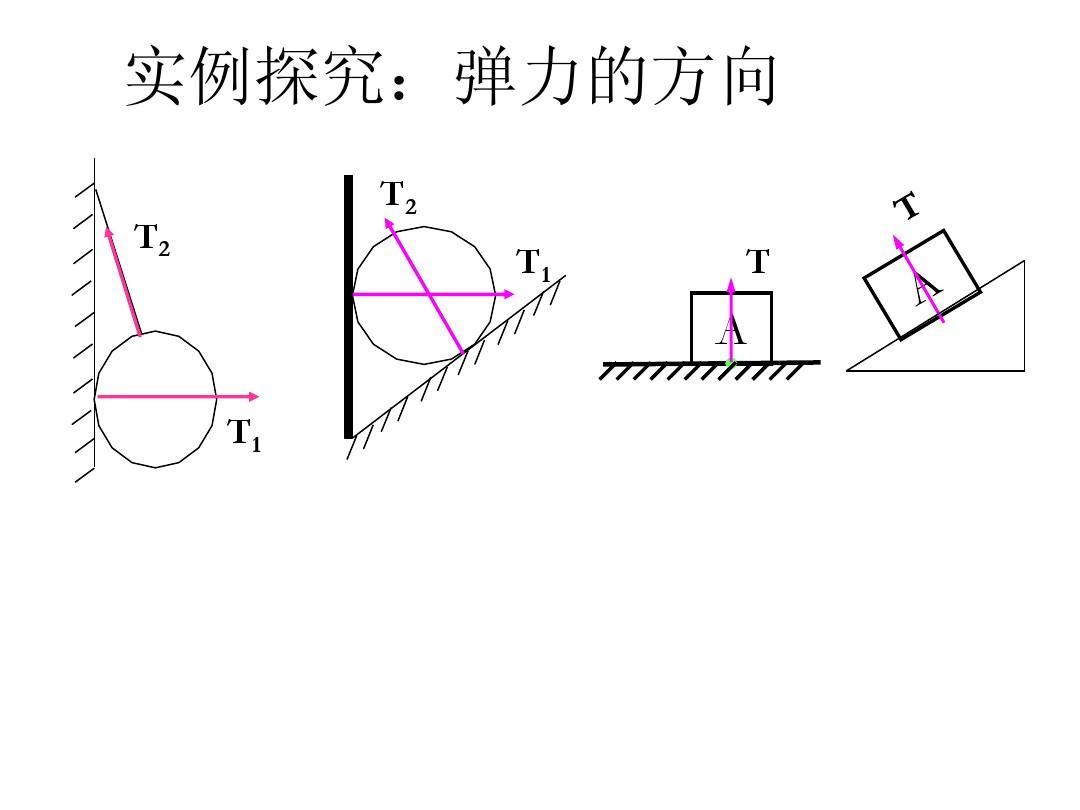胡克定律

虎克的表情 s定律是 f=k·x或 △F=k·δ x，其中 k是 的常數，是 的物體的剛度（倔強）系數。在國際單位制中， F的單位是 牛，X的單位是 米，這是一個形變變量（彈性形變） k的單位是牛/米。剛度系數等于彈簧伸長值（或縮短）單位長度彈性力。

彈性定律是胡克定律之一最重要的發現和最重要的力學基本定律之一。在現代，它仍然是物理學的重要基礎理論。胡克 彈性定律表明：當彈簧彈性變形時，彈力Ff和彈簧的伸長（或壓縮量）x成正比，即F= -k·x 。k是物質的彈性系數，由物質的性質決定，負號表示彈簧產生的彈力及其伸長量（或壓縮）的方向相反。

為了證明這個定律，胡克還做了大量的實驗，用各種材料做了各種形狀的彈性體。

滿足胡克定律的彈性體s定律是一種重要的物理理論模型，是對現實世界中復雜的非線性本構關系的線性簡化，實踐證明在一定程度上是有效的。然而，現實中有很多例子并不能滿足虎克 的法律。胡克的意義s定律不僅描述了彈性變形和力之間的關系，而且創造了一種重要的研究方法：現實世界中復雜非線性現象的線性簡化在理論物理中很常見。

胡克 的定律可以表達為：

Fn∕S=E·△l∕l。

在公式中，比例系數e成為彈性模量，也是楊氏模量s模量，因為△l∕l ∕ L。它是一個純數字，所以彈性模量和應力有相同的單位彈性模量是描述材料本身的物理量從上面的公式可以看出，如果應力大，應變小，彈性模量就大；反之，彈性模量小。彈性模量反映了材料 抗拉伸或壓縮變形的能力對于某種材料，拉伸和壓縮變形的彈性模量是不同的，但它們是相似的這時候可以認為它們是一樣的下表列出了幾種常見材料的彈性模量。

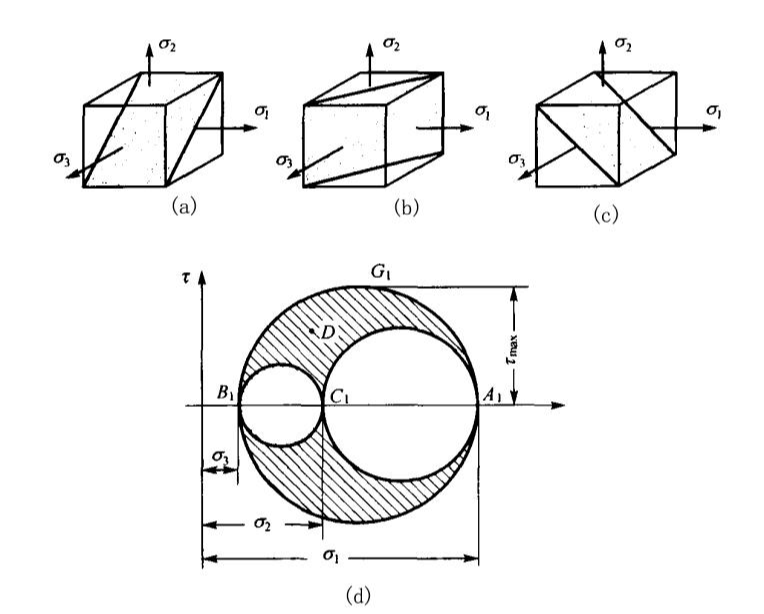胡克 美國法律圖表

材料力學和彈性力學的基本定律之一。由R.胡克在1678年以 命名。胡克 美國法律規定如下：在材料的線彈性范圍內，固體的單軸拉伸變形與外力成正比；也可表述為：當應力低于比例極限時，固體中的應力σ與應變ε成正比，即  σ=ε ε，其中E為常數，稱為彈性模量或Young s模量。廣義虎克 擴展虎克 s定律應用于三維應力和應變狀態。胡克 s定律為彈性力學的發展奠定了基礎。廣義胡克定律有兩種常用的數學形式各向同性材料的s定律：

σ11=λ（ε11 ε22 ε33）2Gε11，σ23=2Gε23，

σ22=λ（ε11 ε22 ε33）2Gε22，σ31=2Gε31，(1)

σ33=λ（ε11 ε22 ε33）2Gε33，σ12=2Gε12，及

其中，σij是應力分量；εij是應變分量（I，j=1，2，3）λ和g是拉梅常數，g也叫剪切模量3356；E為彈性模量（或楊氏模量）v為泊松比。λ、G、e和v之間有如下關系：式（1）適用于已知應變求應力的問題，公式（2）它適用于已知緊張的問題。

根據沒有初始應力的假設，（f 1）0應為零。對于均質材料，材料性質與坐標 無關，所以函數 f 1 對應變的一階偏導數為常數。因此，應力和應變的一般關系式可以簡化如下

上面的關系就是虎克（Hooke）該定律在復雜應力條件下的推廣也稱為廣義虎克 的法律。

廣義胡克定律中的系數Cmns定律（m，n=1，2，…，6）叫做彈性常數，一共36個。

如果物體是由非均質材料制成的，物體中的每一點受力后都會產生不同的彈性效應，所以一般來說，Cmn 是坐標X，Y，z的函數。

然而，如果物體是由均勻材料制成的，那么物體內部的所有點如果受到相同的應力，就會產生相同的應變；相反，如果一個物體中的所有點都具有相同的應變，它們將承受相同的應力。

這個條件反映在廣義虎克定理中，即Cmn 是一個彈性常數。

胡克 彈性定律表明：在彈性極限內，彈簧的彈力F與彈簧的長度變化X成正比，即F= kx。k是物質的彈性系數，由物質的性質決定，負號表示彈簧產生的彈力及其伸長量（或壓縮）的方向相反。

彈簧的串并聯連接

串聯：勁度系數關系1/k=1/k1+1/k2

并聯：剛度系數關系k=k1 k2

注：這串彈簧變得越來越軟和越來越硬，與它們各自的長度無關。

鄭玄-胡克定律

是英國機械師胡克寫的(羅伯特 -1703) 發現于1678年，其實比他更早，1500年前，東漢的儒生教育家鄭玄(公元127-200)對于文章《考工記·馬人》“量其力，有三鈞”在評論里寫:“假設弓勝三石，引三尺，馳其弦，緩其索每增加一塊石頭，就增加一英尺。鄭玄 愛因斯坦的發現比胡克和愛因斯坦早了1500年通過正確地指出力和變形之間的正比例。所以胡克 美國法律應該被稱為“鄭璇——虎克 s定律。

胡克 的發現直接導致了彈簧測力計———測力的基本工具由此誕生，至今仍在物理實驗室廣泛使用。彈簧測力計的原理是“胡克定律”。

虎克 的張量形式s定律。

描述處于三維應力狀態的材料。需要定義一個包含81個彈性常數的四階張量cijkl來連接二階應力張量σij和應變張量(又稱格林張量)εkl。

由于應力張量。應變張量和彈性系數張量之間存在對稱性(應力張量的對稱性是材料力學中剪應力的等價定理)在81個彈性常數中，只有21個與最常見的材料無關。

由于應力的單位尺寸(力/面積)與壓強相同。應變是無量綱的。所以彈性常數張量cijkl中的每一個元素(分量)具有壓力的維度。

新胡克 描述固體材料的大變形力學行為需要s實體模型(neo-虎克固體)和mooney-里夫林實體模型。

彈簧方程

胡克定律

胡克 s定律可以準確描述普通彈簧在變形不太大時的力學行為。

胡克定律應用的一個常見例子法律是春天。在彈性限度內。彈簧的彈力F與彈簧的長度變化X成線性關系。也就是:f=.kx

其中k是彈簧的剛度系數(或稱為倔強系數)它由彈簧材料的性質和幾何形狀決定。負號表示彈簧產生的彈力及其伸長量(或壓縮)的方向相反。這個彈力叫做回復力。表明它有恢復系統平衡的趨勢。滿足上述公式的彈簧稱為線性彈簧。

在線彈性階段，廣義虎克 s定律成立，即應力σ 1 σ p（σp為比例極限）時成立。在彈性范圍內可能不成立，σpσ1σe（σe為彈性極限）雖然在彈性范圍內，廣義虎克 美國法律不成立。

起初，在做實驗的過程中，胡克發現“加在彈簧上的重量與彈簧的伸長成正比”他通過多次實驗證實了自己的猜想。1678年，胡克寫了一篇《彈簧》論文，向人們介紹了彈性物體的實驗結果，為材料力學和彈性力學的發展奠定了基礎。

彈簧測力計

19世紀初，在前人做了大量實驗工作的前提下，英國科學家托馬斯·楊總結了虎克等人的研究成果，并指出：彈性體的伸長超過一定限度，材料就會斷裂，彈力定律就不再適用，彈力定律的適用范圍也就明確指出來了。超出這個應用范圍的形變稱為正則形變）

至此，經過眾多科學家的努力，終于準確地建立了物體的彈力定律。后世稱這條定律為虎克 美國紀念胡克定律的開創性工作和成就。

虎克 的另一個名字s法——鄭玄-胡克定律

胡克 s定律是由英國機械師胡克提出的(羅伯特 -1703) 發現于1678年，其實比他更早，1500年前，東漢的儒生教育家鄭玄（公元127-200）對于文章《周禮·冬官考工記·弓人》“量其力，有三鈞”當一個句子被注釋時，它被寫成《周禮注疏·卷四十二》：讓 s假裝弓比三石，引三尺，馳其弦，緩其索每增加一塊石頭，就增加一英尺。正確地指出了力和變形之間的正比關系愛因斯坦的發現比胡克和愛因斯坦早了1500年南。因此，一些物理學家認為胡克 美國法律應該被稱為“鄭玄-胡克定律”。